Differential steering

Driving Straight

Driving straight is pretty easy. The wheels just have to go the same distance.

What if they don’t go the same distance?

What happens if the left wheel goes slower than the right wheel?

The robot goes in an arc. The wheels draw out 2 different circles with 2 different radii. The arc with the smaller radius (\(r1\), the white line) has a smaller circumference. That means the left wheel has driven a smaller distance. It has gone slower.

How would you drive in an arc with a given radius?

We know the wheels trace out arcs when we make the wheels go at different speeds, but how do we decide what the wheel speeds should be?

What do we know?

Let us start with what we know about the two arcs, and the arc we want the center of the robot to go through.

The first thing we can say about any circle is that the radius is proportional to the circumference. This means that the inner and outer arc lengths are proportional to the inner and outer radii, or

\[\frac{leftWheelDistance}{rightWheelDistance} = \frac{r1}{r2}\]

This is the same as saying that

\[ratioBetweenWheelSpeeds = \frac{r1}{r2}\]

Hey! We found out what the ratio between the wheel speeds is supposed to be if we know the two radii. But how do we find what the two radii are? We only know what we want the radius of the orange circle to be.

But we know what the distance between the two wheels are.

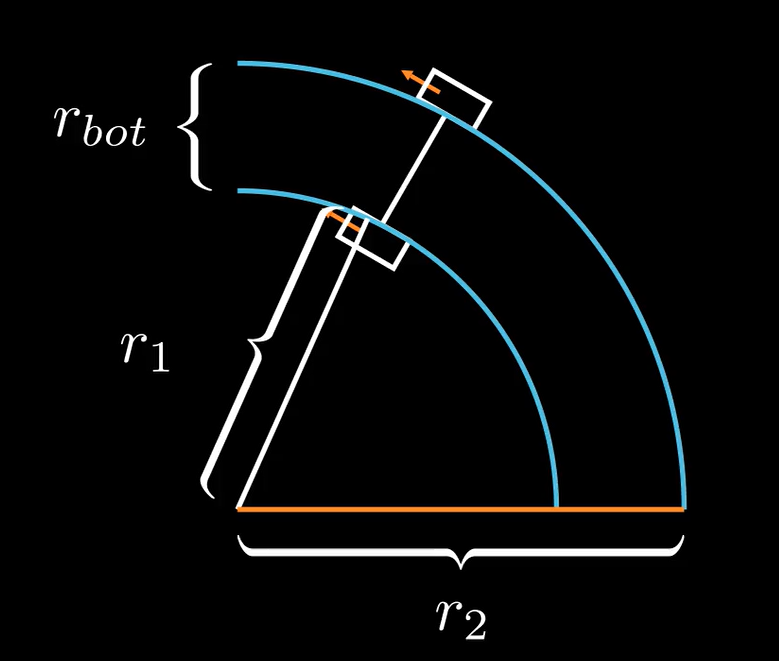
../../_images/Screenshot2023-03-07142430.png

If \(r_{bot}\) is the distance between the two wheels, then

\[r_1 = r_{desired} - \frac{r_{bot}}{2}\]

since r1 is less than the desired radius, and

\[r_2 = r_{desired} + \frac{r_{bot}}{2}\]

We found out the radii of the circles we want the left and right wheels to trace, and we know how to find the ratio between the wheel speeds from that.

Remember: .. math:: ratioBetweenWheelSpeeds = frac{r1}{r2}

Putting them together, we get,

\[ratioBetweenWheelSpeeds = \frac{leftWheelSpeed}{rightWheelSpeed} = \frac{r_{desired} - \frac{r_{bot}}{2}}{r_{desired} + \frac{r_{bot}}{2}}\]

Try it yourself

Try it yourself! Make your robot drive in a circle. Choose the radius of the circle to be whatever you want!

What will you set your wheel efforts to? Does it drive in a circle?

What happens if you set the wheel efforts to half of what you decided in part a?

What happens if you flip the wheel efforts (set the left wheel effort to what you decided as the right wheel effort and vice-versa)?

Additional challenges

Try to make the robot do a point turn! What is the radius of the circle that you want it to drive in then?: (Try drawing the robot and the point you want it to turn around. What can you infer about it then?)

Try and make the robot turn around one of the wheels. What is the new desired radius?

Try making the robot drive backwards in an arc